목 차
1. 들어가며
2. 사전설명
1) 경사하강법 설명
2) 데이터 관리
3. 코드설명
4. 마치며
1. 들어가며
지난글에서는 선형회귀분석의 개념에 대해 알아보았다. 필자도 정확히 이해할 수 없어서 대략적인 설명을 했다. 선형회귀에 관심이 있다면, 인터넷 검색 또는 서적(book)을 통해 깊이 공부해보면, 선형회귀 개념에 대해 어느정도 감은 가질 수 있을 것이다.
이번글에서는 케라스, CNN 등의 라이브러리의 도움없이, 선형회귀분석 중 경사하강법을 이용하여 y = wx + b 선형회귀의 w(가중치 weight, 기울기) 및 b(편향 bias, y절편)을 각각 구해보자.
※ 코드 출처 : 또야님 티스토리에서 경사하강법 설명
(코드의 주소는 "한글"로 설정이 되어 있어서 그 주소가 상당히 길기 때문에 링크를 누르면 연결되게끔 기재한다)
2. 사전설명
1) 경사하강법 설명
경사하강법은 y = ax^2 (아래로 볼록)한 이차 함수에서 기울기가 0 혹은 최소인 m을 학습을 통해 찾는 방법이다. < 그림1 >에서 a1의 오차보다 m의 오차가 작은 것을 확인할 수 있다.
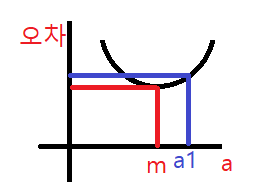
2) 데이터 관리
자, 간단한 3줄의 데이터를 이해해보자.
data = [[2, 81], [4, 93], [6, 91], [8, 97]] # 데이터셋 설정
x = [i[0] for i in data] # [2, 4, 6, 8]이 됨
y = [i[1] for i in data] # [81, 93, 91, 97]이 됨
1줄 : 데이터 모음은 리스트 태형으로 리스트 내 리스트를 썼다. [ [2,81], ..]의 형태이며, 2는 x절편, 81은 y절편이다.
2줄~3줄 : 필자의 경우 for문을 풀어서 쓰는 편인데, 아래에서 설명할 코드는 리스트 내 for문을 사용하였다.
2줄의 내용을 확인해 보자.
x = [i[0] for i in data] # [2, 4, 6, 8]이 됨
2줄 : for i in data이다. 1줄에서 data는 리스트 태형이다. 리스트 태형에서 1번째 요소([2,81]), 2번째 요소([4,93]) 등을 순차적으로 뽑아온다. i[0]을 통해 1번째 요소 중 1번째 요소(2,81 중 2를 말한다)를 추출하라는 뜻이다. 개인적으로 굉장히 멋진 코드라고 생각했다. 필자에게 구현해보라고 하면, 수십번을 고민했을 코드이다. @.@
3. 코드설명
30줄 남짓이다. 천천히 따라하다보면, 이해할 수 있을 것이다.
※ 코드 출처 : 또야님의 티스토리 中 경사하강법 설명
(코드의 주소는 "한글"로 설정이 되어 있어서 그 주소가 상당히 길기 때문에 링크를 누르면 연결되게끔 기재한다)
import matplotlib.pyplot as plt
import numpy as np
data = [[2, 81], [4, 93], [6, 91], [8, 97]] # 데이터셋 설정
x = [i[0] for i in data] # [2, 4, 6, 8]이 됨
y = [i[1] for i in data] # [81, 93, 91, 97]이 됨
x_data = np.array(x) # 넘파이 배열로 변환
y_data = np.array(y)
a = 0 # 기울기 a를 0으로 초기화
b = 0 # y절편 b를 0으로 초기화
lr = 0.05 # 학습률 설정 (learning rate)
epochs = 2000 # 반복 횟수 설정
# 경사 하강법 시작
for i in range(epochs):
y_pred = a * x_data + b # y 예측 값을 구하는 식
error = y_data - y_pred # 오차 error = y 값 - y 예측 값
a_diff = -(1 / len(x_data)) * sum(x_data * (error)) # 평균 제곱 오차를 a로 미분한 값
b_diff = -(1 / len(x_data)) * sum(y_data - y_pred) # 평균 제곱 오차를 b로 미분한 값
a = a - lr * a_diff # 학습률 * 미분 결과 후 기존 a 값 업데이트
b = b - lr * b_diff # 학습률 * 미분 결과 후 기존 b 값 업데이트
if i % 100 == 0: # epoch가 100번 반복될 때마다 아래의 내용을 출력
print("epoch = %.f, 기울기 = %.04f, 절편 = %.04f, 에러 = %.04f" % (i, a, b, error.mean()))
plt.scatter(x, y) # 이하 그래프 출력
plt.plot([min(x_data), max(x_data)], [min(y_pred), max(y_pred)])
plt.show()
1줄~2줄 : 데이터(4줄~6줄)를 통한 그래프를 그리기 위한 matplotlib 라이브러리 및 숫자배열 변환을 위한 numpy를 임포트한다.
4줄~6줄 : 위에서 설명한 데이트셋 및 리스트 내 for문을 활용하여 데이터 추출 방법이다.
8줄~9줄 : 5줄 x_데이터 및 6줄 y_데이터를 넘파이 배열로 변환한다.
11줄~12줄 : 기울기 a 및 y절편 b를 각각 0으로 초기화한다.
14줄 : 학습률(learning rate)을 최초 0.05로 설정한다. 여기서 성향차이가 있다. 양수를 기준으로 하는 경우 5% 정도 오차를 기준으로 학습을 한다. 개인적으로 해외선물을 학습시킬 때 학습률 0.05는 조금 큰 값으로 생각된다. 양수의 1틱 차이가 1일 때, 해외선물 나스닥의 1틱당 차이는 0.25이다. 개인의 취향이겠지만, 해외선물의 학습률은 0.05보다는 작은 값으로 해야할 것으로 보인다.
근데, 학습률이 무엇인가? 간단하게 생각하자. 1회 시행후, 2회 시행때 임의로 던져보는 값(=조정값?)의 개념으로 생각하면 된다. 0.05를 더하거나 빼서 근사치에 가까운지 시험해 본다고 이해하면 될 것이다. 0.05씩 계속 조정하면서 근사치에 가까워진다고 생각하자.
16줄 : 반복횟수는 2000으로 설정한다.
19줄 : 경사하강법에 대한 코드이다. 필자도 정확히는 설명 못하였다.ㅠ
또야님의 경사하강법을 참고하자. 또다른 좋은 설명으로 유튜버 테디노트님의 영상이 있으니, 개념을 숙지할 때 참고하자.
※ 유튜버 테디노트님의 경사하강법 설명 : https://www.youtube.com/watch?v=GEdLNvPIbiM
20줄 : y_pred 값을 구한다. 우리는 epoch 2000회 반복을 통해 20줄의 함수 내 a, b 값을 구한다.
21줄 : 오차 error = y값 - y예측값이다. ※ 즉, 오차는 (y_실제값) - (y_예측값)으로 구한다.
23줄~27줄 : 여기는 또야님의 티스토리 내 경사하강법 설명을 참고하자. 애석하게도 필자는 편미분의 개념을 잘 모른다. ㅠㅠ
23줄~24줄 : a(기울기) 및 b(y절편)를 평균제곱오차를 a로 미분한 값을 각각 구한다.
26줄~27줄 : 학습률 x 미분 결과 후 기존 a값, b값을 업데이트 한다.
29줄~30줄 : epoch가 100번일 때마다, 30줄을 출력한다.
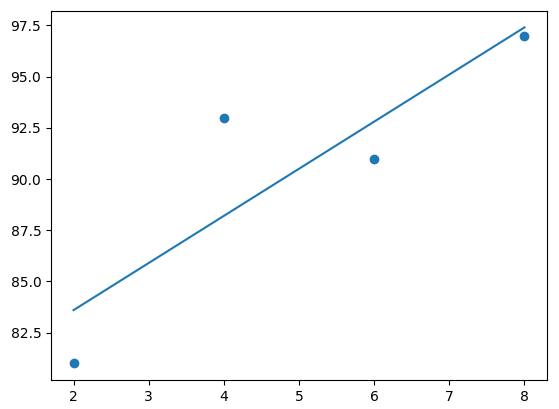
32줄 : 5줄 및 6줄의 x, y 데이터를 활용하여 그래프를 그린다.
33줄 : 19줄~27줄 사이에서 5줄(x 데이터) 및 20줄(y예측 최대값, 최소값)을 통해 그래프를 그린다.
34줄 : 그래프를 보여달라
파이참의 결과창에 나타난 값은 아래와 같다. epoch(반복횟수)가 증가할수록 기울기, y절편이 2.3 및 79로 수렴하는 것을 알 수 있다. 또한 에러는 0으로 수렴한다.
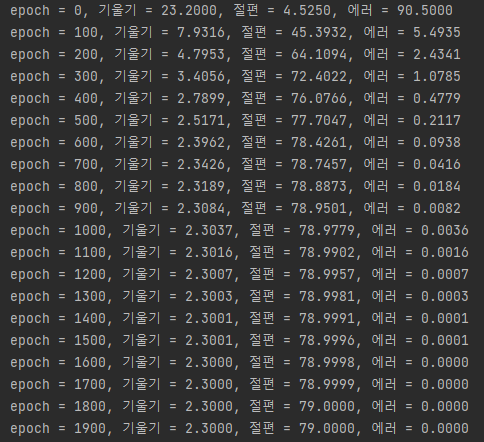
다만, < 그림3 >에서 1900회까지만 출력된 이유는 20줄에서 반복을 2000회로 설정하였다. for문에서 range(2000)이면 0~1999까지만 2000회이다. 즉, i= 0 ~ 1999까지만 실행된다. 2000회를 보고 싶으면 20줄을 아래(2줄)와 같이 수정한다.
총 2001회를 반복하지만, 출력될 때는 i = 2000일 때 값이 출력된다.
for i in range(epochs):
for i in range(epochs + 1):
4. 마치며
위 코드의 예시는 비교적 간단한 코드이다. 데이터가 많아지면, 에러 등 오차값이 커진다. 적당 수준을 알 수는 없겠지만, 데이터 수준에 맞는 학습률 및 반복횟수 설정을 통해 지혜롭게 기울기와 y절편을 구해보자.
해외선물 자동매매를 통해 수익은커녕 손실이 계속 발생하는데도, 자동매매를 포기하지 못한 가장 큰 이유는 수동매매(손매매)에 대한 "내자신(myself)"의 실력에 대한 깊은 회의를 느꼈기 때문이다. 아무리 차트와 호가창을 보고 있어도, 손실이 누적되니 수동매매(손매매)를 할 자신감이 떨어진다.
또다른 이유로, 자동매매를 구축하는 것은 코딩 그 자체가 재미있기 때문이다. pc 앞에 앉아 "수익에 대한 희망"을 가진채 코드를 작성할 때는 시간가는 줄 모른다. pc게임에 이렇다할 흥미가 없어진 요즘, 수없이 고민하고 코드로 구현해 보았을 때의 셀레임을 느껴본 사람은 코딩을 쉽게 포기하지 못한 이유가 될 것이다.ㅎㅎㅎ
지금도 마찬가지로 약간의 희망은 가지고 있다. 1분봉의 종가 데이터 모음을 통해 그래프를 하루 빨리 그려보고 싶다. 경사하강법이 100% 수익을 보장해주지는 않을 것이다. 다만, 그 동안 막혔던 추세 파악 및 변곡점(y 절편)을 찾을 수 있을 것 같다는 "행복회로"가 머리 속에서 떠나지 않으니, 설레일 뿐이다. 물론 경사하강법을 통한 선형회귀 선(line)을 찾는다고 하더라도, 손실로 이어질 수 있겠지만... 그래도 이 희망의 끈을 쉽게 놓고 싶지 않다.ㅎㅎㅎ
세상은 고민한 만큼 보인다. 해외선물 수익을 위해 꾸준히 고민하고, 인내심을 가지면서 코드를 작성해 보자~!
'2. 해외선물 > 2-2. 해외선물 알고리즘 연구' 카테고리의 다른 글
| (해외선물 자동매매) 차트 지지/저항 구하기 (2) 벽돌깨기 게임 학습하기 (0) | 2024.10.05 |
|---|---|
| (해외선물 자동매매) 차트 지지/저항 구하기 (1) 벽돌깨기 게임 구현하기(BricksBreak) (1) | 2024.10.04 |
| (해외선물 자동매매 알고리즘) (2) 역전파(backpropagation) 알고리즘 구현하기 (6) | 2024.02.08 |
| (해외선물 자동매매 알고리즘) (1) 역전파(backpropagation) 구현을 위한 numpy 이해하기 (2) | 2024.02.07 |
| (해외선물 자동매매 알고리즘) (1) 선형회귀분석 설명 (개념설명) (2) | 2024.01.29 |
| (해외선물 자동매매 알고리즘) (3) MCTS를 활용하여 틱택톡 만들기 (2) | 2024.01.22 |
| (해외선물 자동매매 알고리즘) (2) 틱택톡 만들기 (컴퓨터와 대결) (2) | 2024.01.01 |
| (해외선물 자동매매 알고리즘) (1) 틱택톡 만들기 (2) | 2023.12.31 |